
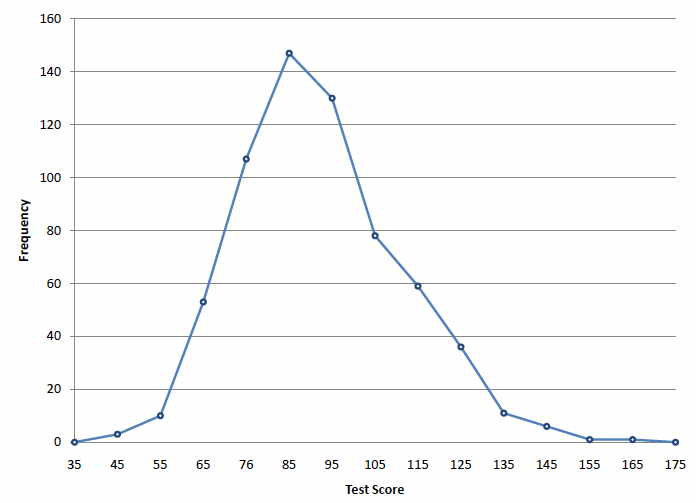
Full details of its theoretical underpinning can also be found in Stuart & Ord (1991). An introduction to the basic principles of MLE, the E-M and other methods, can be found in Everitt (1987). Examples of its use in quantal analysis of synaptic currents and the analysis of single-channel currents can be found in the next chapter. The algorithm iterates between these two processes, until the parameters cease to change between steps. Using these values, a new (and better) set of parameters is estimated by working backwards from the posterior probabilities for each data point (maximisation step). mixture, based upon an initial set of guesses for the p.d.f. To start, it estimates the (posterior) probability of each data point, x i, belonging to one or other components of the p.d.f. The E-M algorithm is also an iterative method, but it avoids directly searching the parameter space for the LL maximum. It suggests that 37% (a 0 = 0.37) of the MEPCs in the recording arise from a population with a mean amplitude of μ 0 × 2.54 and a standard deviation of σ 0 = 0.56 nA, while the remainder come from a population with a mean of μ 0 = 4.8 and standard deviation σ 1 = 1.29 nA.Īnother method commonly used to maximise the likelihood function is the expectation-maximisation (E-M) algorithm, developed by Dempster et al. It was obtained by maximising LL(θ) (with n = 2 in equation ) using a version of the simplex algorithm, built into the Matlab program. The maximum likelihood estimate for the mixture of two gaussians which best fits the distribution of MEPC amplitudes is shown superimposed on the frequency histogram in Fig. A discussion of maximum likelihood estimation can be found (in the context of single-channel current analysis) in Colquhoun & Sigworth (1995). The same kind of convergence and numerical stability issues that arose in relation to non-linear least squares curve fitting also apply to likelihood maximisation.

The simplex algorithm which was discussed in Section 6.6.2, or gradient-based optimisation methods (but not the L-M method, which is specific to least squares problems) are often used to iteratively search the LL function space for the maximum. A number of approaches can be taken to maximising the log-likelihood function. Which has its maximum at the same point as the likelihood function itself. Figure 6.22b shows the frequency histogram of the MEPC amplitudes, computed over a 0–10 nA range, split into 50 bins, each 0.25 nA wide.
Cumulative frequency histogram maker series#
The range of amplitudes in the experiment is split into a series of equal-sized subranges, or histogram bins, and the number of amplitude measurements falling into each bin is counted. This can be better revealed by plotting the distribution of MEPC amplitudes in the form of a frequency histogram. One important question to be considered when presented with data like this is whether the observed amplitude distribution arises from a single, homogeneous population of MEPCs or from a mixture of populations with different characteristics. In this particular circumstance, it is also due to an inherent variability of the amplitude of the MEPC signal itself. This is partly due to the poor signal-noise ratio, usually unavoidable in such recordings, even with optimal low-pass filtering. It can be seen that the measured amplitudes vary randomly from record to record over quite a wide range of values (1.2-10 nA). 6.9, recorded from a snake neuromuscular junction. Figure 6.22(a), for instance, shows the peak amplitudes measured from a series of 4300 miniature endplate current signals, similar to those in Fig.


 0 kommentar(er)
0 kommentar(er)
